Alogorithm(알고리즘)

어떠한 문제를 해결하기 위한 일련의 절차를 공식화한 형태로 표현한 것
프로그래밍에서 알고리즘은 input 값을 통해 output 값을 얻기 위한 계산 과정
문제를 해결할 때, 정확하고 효율적으로 결과값을 얻기 위해서 알고리즘이 필요하다.
알고리즘의 조건
- 입력 : 외부에서 제공되는 자료가 0개 이상 존재한다.
- 출력 : 적어도 2개 이상의 서로 다른 결과를 내어야 한다. (모든 입력에 하나의 출력이 나오면 안 된다.)
- 명확성 : 수행 과정은 명확하고 모호하지 않은 명령어로 구성되어야 한다.
- 유한성 : 유한 번의 명령어를 수행 후 유한 시간 내에 종료한다.
- 효율성 : 모든 과정은 명백하게 실행 가능(검증 가능)한 것이어야 한다.
좋은 알고리즘의 기준
- 정확성 : 적당한 입력에 대해서 유한 시간내에 올바른 답을 산출하는가를 판단.
- 작업량 : 전체 알고리즘에서 수행되는 가장 중요한 연산들만으로 작업량을 측정. 해결하고자 하는 문제의 중요 연산이 여러 개인 경우에는 각각의 중요 연산들의 합으로 간주하거나 중요 연산들에 가중치를 두어 계산
- 기억 장소 사용량 : 수행에 필요한 저장 공간
- 최적성 : 그 알고리즘보다 더 적은 연산을 수행하는 알고리즘은 없는가? 최적이란 가장 '잘 알려진' 이 아니라 '가장 좋은'의 의미이다
- 복잡도 (점근 표기법 : Big-O Notation) :알고리즘이 소모하는 소요 시간과 메모리 사용량 등의 자원이다. 전자를 시간 복잡도, 후자를 공간 복잡도라 한다.
 |
빅오 표기법 | 내용 |
| O(1) | 입력 자료의 수에 관계없이 일정한 실행 시간을 가짐 | |
| O(log N) | 입력 자료의 크기가 N일경우 log2N 번만큼의 수행시간을 가짐 | |
| O(N) | 입력 자료의 크기가 N일경우 N 번만큼의 수행시간을 가짐 | |
| O(N log N) | 입력 자료의 크기가 N일경우 N*(log2N) 번만큼의 수행시간을 가짐 | |
| O(N2) | 입력 자료의 크기가 N일경우 N2 번만큼의 수행시간을 가짐 | |
| O(N3) | 입력 자료의 크기가 N일경우 N3 번만큼의 수행시간을 가짐 | |
| O(2n) | 입력 자료의 크기가 N일경우 2N 번만큼의 수행시간을 가짐 | |
| O(n!) | 입력 자료의 크기가 N일경우 n*(n-1)*(n-2)... * 1(n!) 번만큼의 수행시간을 가짐 |
알고리즘의 분류
주제별 분류
정렬(Sort)
1. 버블정렬(Bubble)
- 인접한 두 데이터의 크기를 비교하여 정렬하는 알고리즘

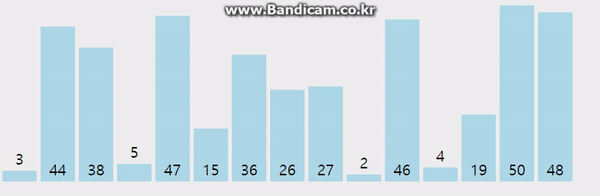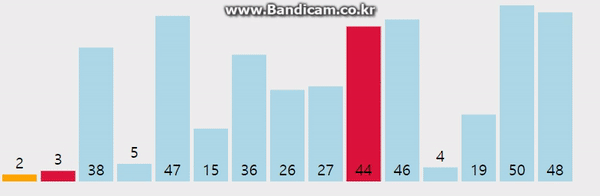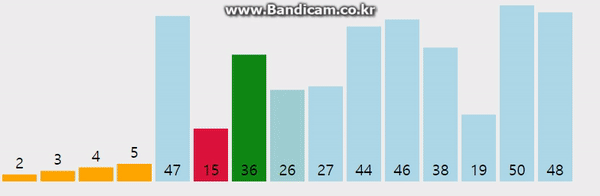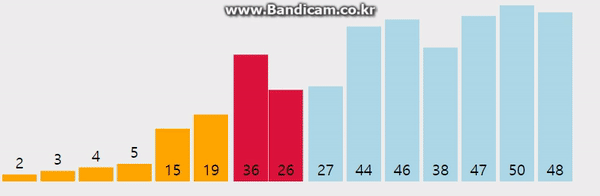
2. 선택 정렬(Selection)
- 주어진 데이터 중 최소값을 찾아 순서대로 정렬하는 알고리즘
- 후보군 중 최소값을 찾아낸 후, 맨 앞의 데이터와 교체한다.
- 교체된 맨 앞의 데이터를 제외한 나머지 후보군에서 다시 최소값을 찾아낸다.
3. 삽입 정렬(Insertion)
- 1번 index에 위치한 데이터를 기준으로 해당 데이터의 앞 쪽에 위치한 데이터와 비교한다.
- 더 작은값을 찾을 때까지 데이터를 뒤로 밀어내어 정렬하는 알고리즘
- 삽입된 데이터보다 작은 데이터를 만날 때까지 반복한다. 없는 경우, 0번 index에 위치하게 된다.

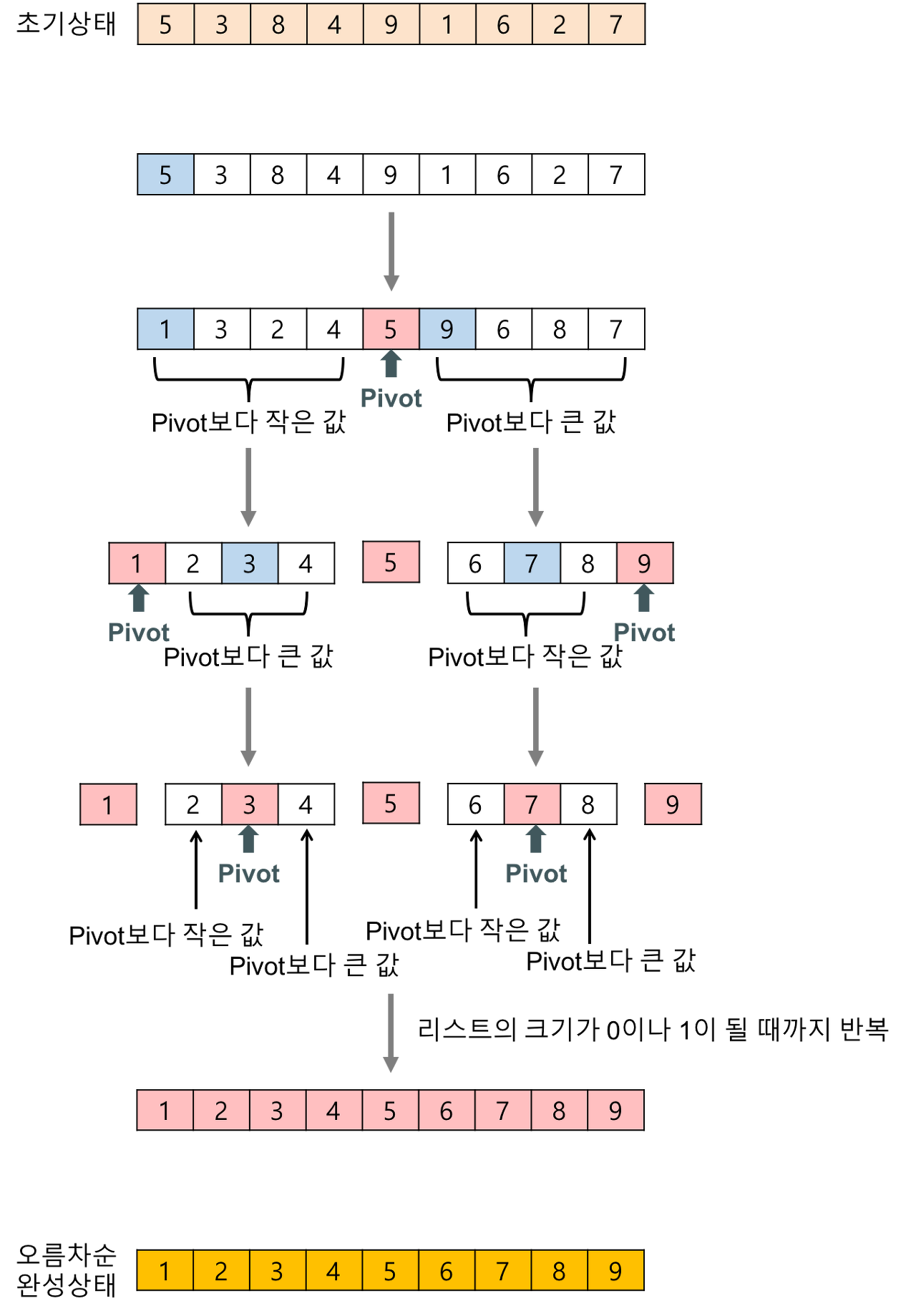
4. 퀵 정렬(Quick)
- 데이터에서 기준점(pivot)을 정하여 pivot보다 작다면 좌측(left)에, 크다면 우측(right)에 정렬한다.
- 좌/우측으로 1차 정렬된 데이터에서 좌/우측 각각의 pivot을 다시 선정하고 정렬을 수행한다.
- 이 과정을 재귀함수를 사용하여 반복하며, 최종적으로 정렬된 데이터를 반환한다.
5. 병합 정렬(Merge)
- 분할 정복 알고리즘을 기반한 정렬이며, 재귀함수를 사용한다.
- 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.

탐색(Search)
1. 이진 탐색(Binary Search)
- 탐색할 자료를 반으로 나누어 찾는 데이터가 있을만한 곳을 탐색하는 방법
2. 순차 탐색(Sequential Search)
- 데이터가 담겨있는 리스트를 앞에서부터 하나씩 순차적으로 비교하여 원하는 데이터를 찾는 방법

그래프(Graph)
1. 너비우선탐색(BFS)
- 정점(노드)과 같은 레벨에 있는 노드(=형제 노드)를 먼저 탐색하는 방식

2. 깊이우선탐색 (DFS)
- 정점(노드)의 자식노드를 먼저 탐색하는 방식

3. 최단경로 알고리즘(Shortest Path Algorithm)
- 그래프에서 두 노드를 잇는 가장 짧은 경로를 찾는 알고리즘이다.
- 간선(edge)의 가중치 합이 최소인 경로를 찾는 것이 목적이다.
- 최단경로 알고리즘에는 3가지 문제유형이 있다.
| a) 단일출발(single-source) : 특정 노드와 그 외 노드간의 최단경로 b) 단일출발 및 단일도착(single-source & single-destination) : 특정 노드 2개의 최단경로 c) 전체 쌍(all-pair): 모든 노드간의 연결조합에 대한 최단경로 |
4. 다익스트라 알고리즘(Dijikstra Algorithm)
- 최단경로 알고리즘에서 단일출발에 해당한다.
- 첫 정점을 기준으로 연결되어 있는 인접노드를 추가해가며 최단거리를 갱신하는 방법이다.
- 다익스트라 알고리즘 중 가장 개선된 알고리즘이 우선순위 Queue를 활용한 것이다.


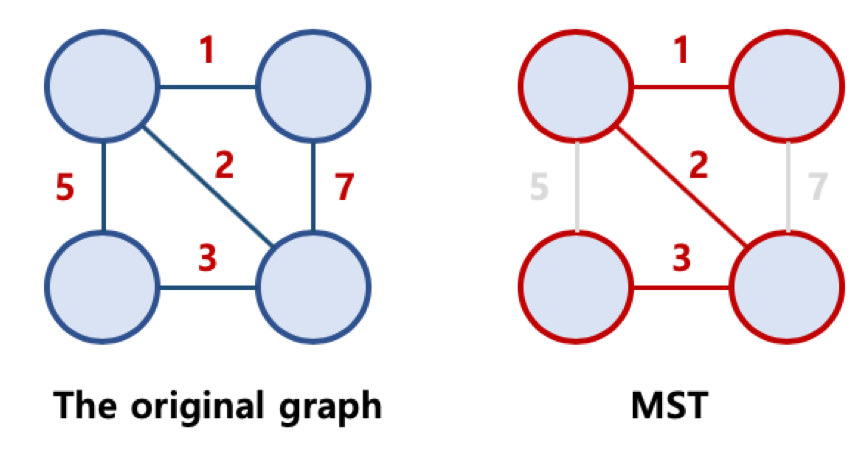
5. 최소신장트리 알고리즘(Mnimum Spanning Tree)
- 신장트리란, 그래프 내부의 모든 노드가 연결되어 있으며, 사이클이 없는(트리의 속성) 그래프를 말한다.
- 최소신장트리란, 간선의 가중치 합이 가장 작은 경로로 이루어진 신장트리를 말한다.
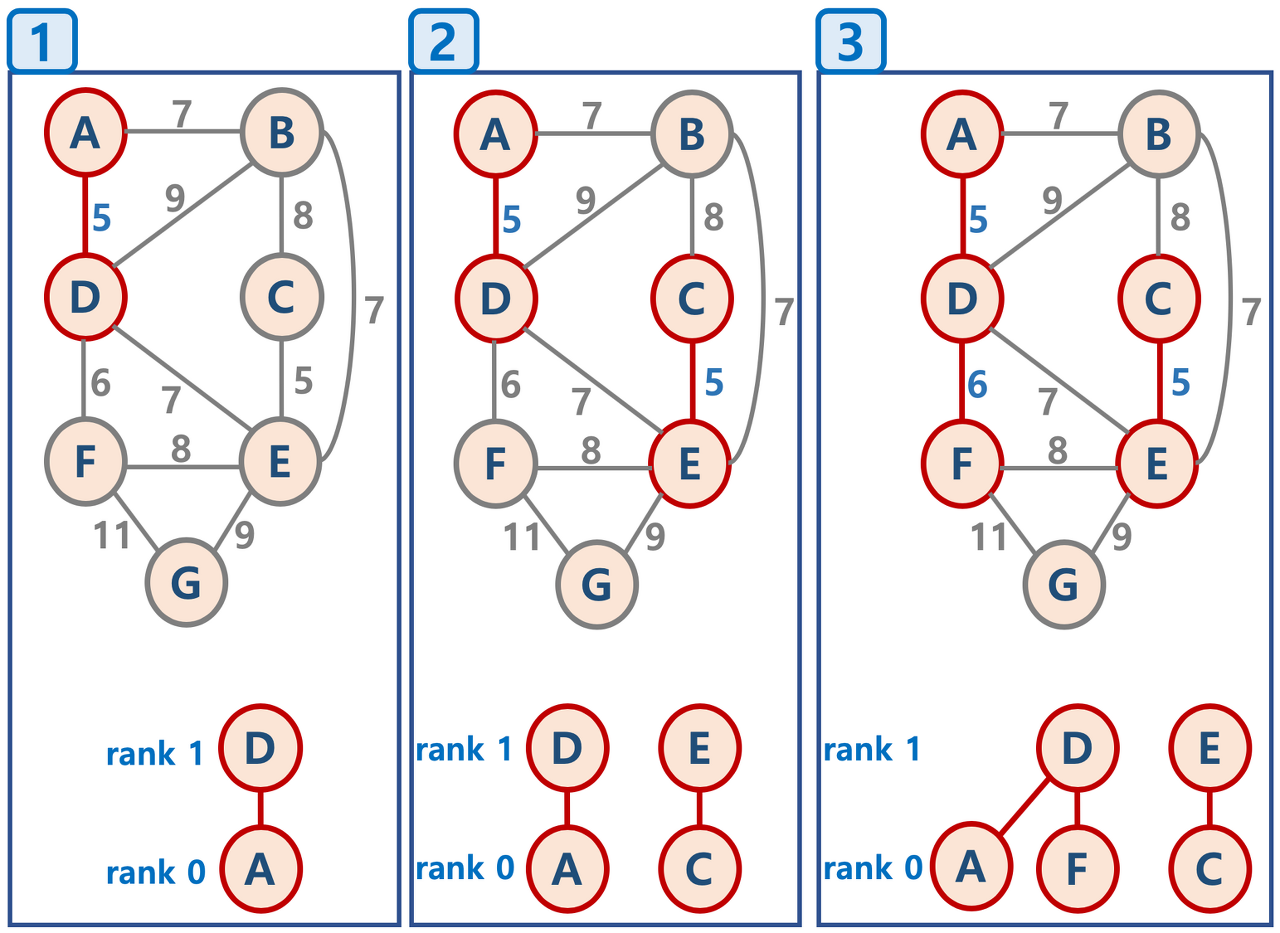
6. 크루스칼 알고리즘(Kruskal's Algorithm)
- 대표적인 최소신장트리 알고리즘으로, 탐욕 알고리즘을 기반하여 선택과 결정을 하는 방식이다.
- 모든 간선의 가중치를 오름차순으로 정렬 후 가장 낮은 가중치를 갖는 간선부터 모든 노드를 연결하며 MST를 찾는다.
- 사이클의 유무를 판단하기 위해 Union-Find 알고리즘을 사용한다.

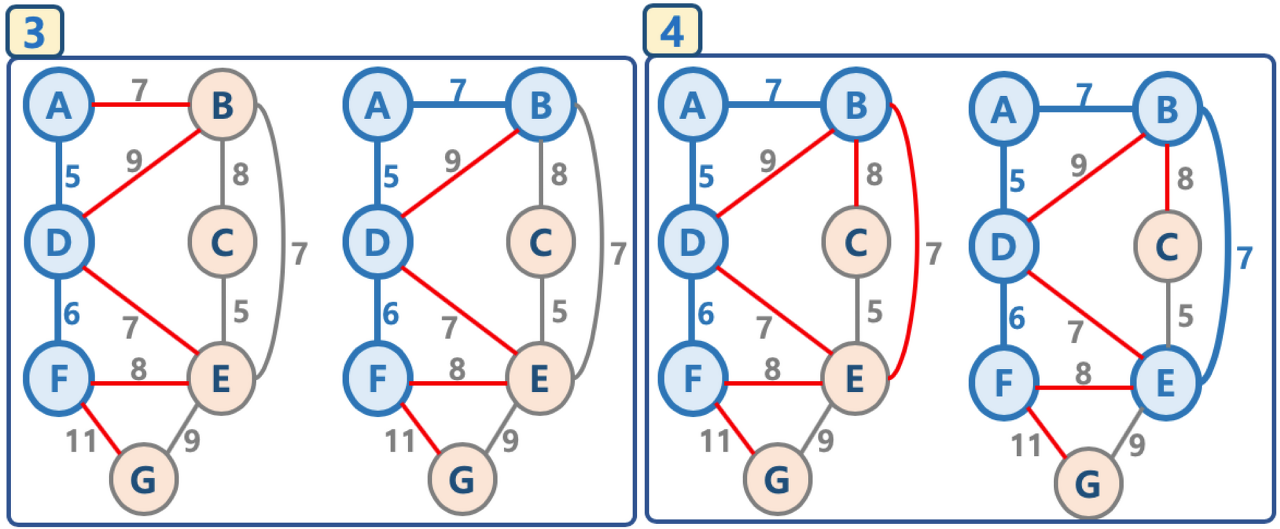
7. 프림 알고리즘 (Prim's Algorithm)
- 크루스칼 알고리즘과 마찬가지로, 대표적인 최소신장트리 알고리즘이며 탐욕 알고리즘을 기반으로 한다.
- 어떤 노드와 인접한 노드의 간선만을 대상으로 하여, 인접노드 중에서 간선의 가중치가 가장 작은 간선을 선택하여 해당 인접노드를 연결하는 방식으로 MST를 찾는다.

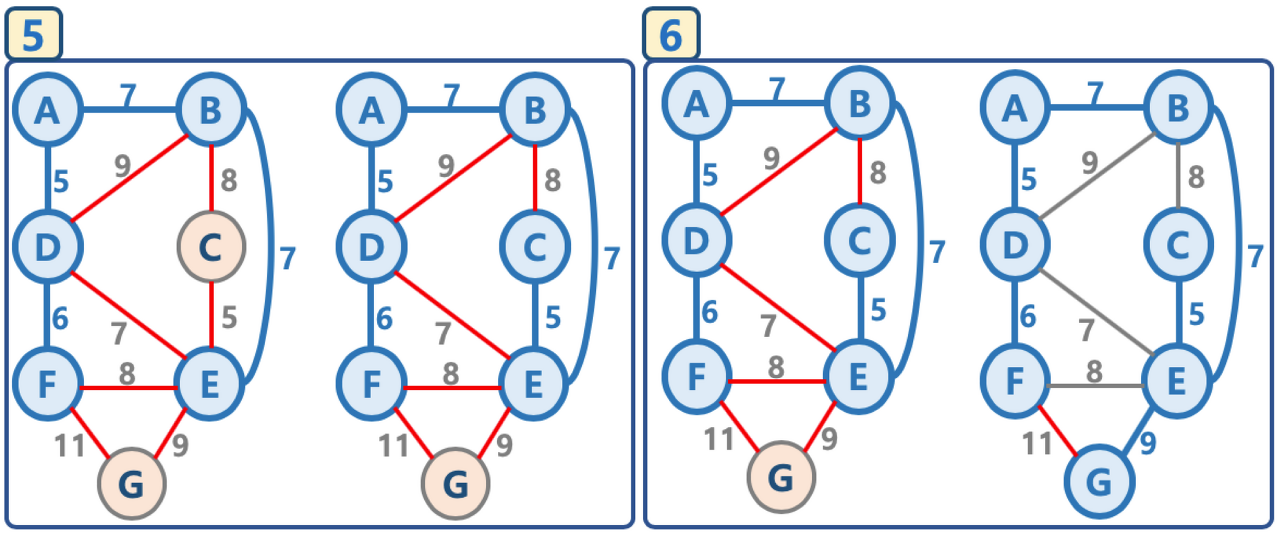
8. 개선된 프림 알고리즘(Improved Prim's Algorithm)
- 개선된 프림 알고리즘은 간선이 아닌 노드를 중심으로 우선순위 큐를 적용하는 방식이다.
- 개선된 프림 알고리즘은 노드를 기준으로 하여 E log V 만큼의 시간복잡도를 갖는다. 그래프는 노드 보다 간선의 수가 더 많기 때문에 그 차이만큼 반복연산이 줄어들어 시간복잡도가 개선되었다.
설계 기법/전략/패러다임에 의한 분류
알고리즘 문제해결전략(Problem Solving Strategy)
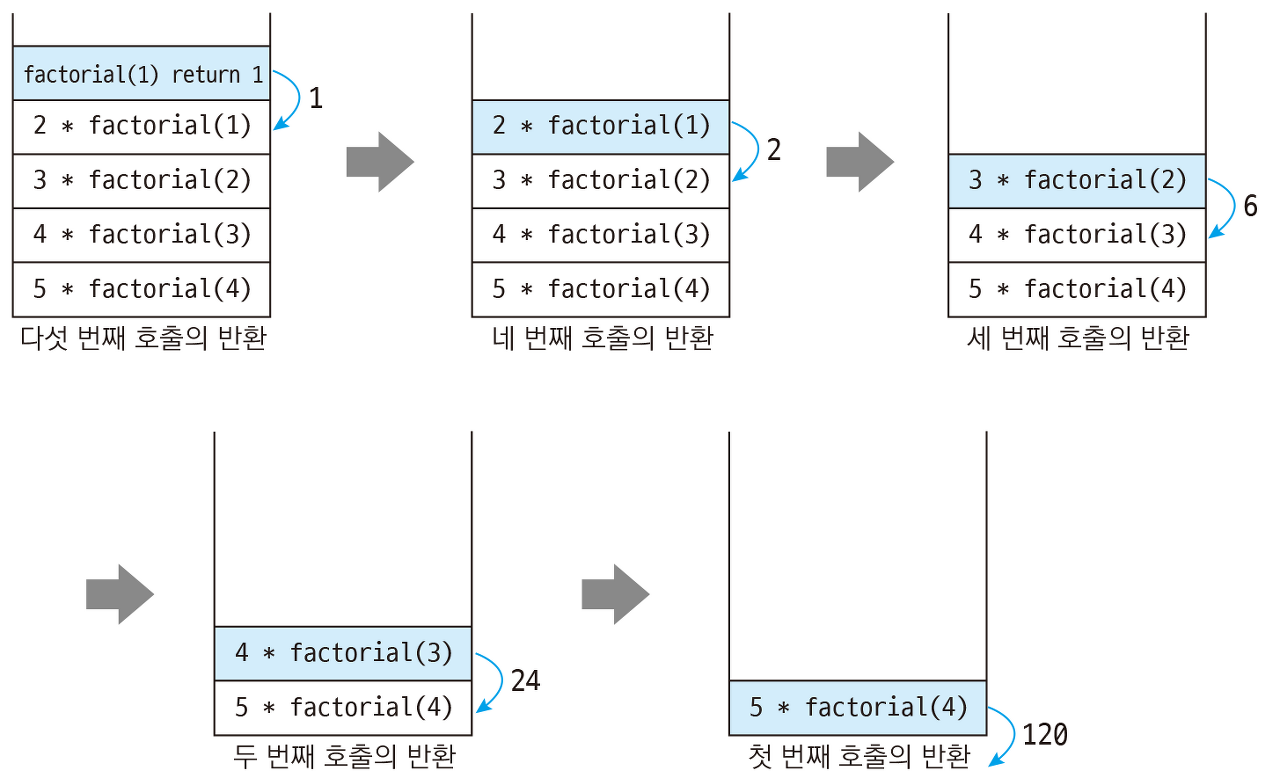
1. 재귀호출(Recursive Call)
- 함수 안에서 해당 함수가 호출되는 형태를 말한다.
- 재귀함수는 마치 Stack처럼 동작한다고 생각하면 이해하기가 편하다.

2. 동적계획법(Dynamic Programming)
- 하나의 큰 문제를 해결하기 위해서 큰 문제를 작은 문제로 나누어 해결한 후, 작은 문제로부터 계산된 결과값를 이용하여 전체문제를 해결하는 알고리즘
- 상향식 접근법 : 가장 최하위 문제의 답을 구한 후, 이를 이용하여 상위 문제를 풀어나가는 방식
- 메모이제이션(Memoization) : 프로그램 실행시, 중복되는 연산이 2번 수행되지 않도록 이전에 계산한 값을 저장하여 전체적인 연산실행속도를 빠르게 하는 기술
| 동적계획법을 사용하는 이유 큰 문제를 풀다보면 중복되는 연산이 발생하게 된다. 이 중복연산을 제거하고 재활용하여 전체적인 코드의 수행 및 연산 효율을 증대시키기 위함이다. |
3. 분할 정복(Divide & Conquer)
- 하나의 큰 문제를 해결하기 위해, 작은 문제로 나누어 하위문제를 해결하고 다시 병합하여 상위문제의 답을 얻는 방식
- 하향식 접근법: 상위 문제의 답을 구하기 위해, 아래로 내려가면서 하위문제의 해답을 먼저 구하는 방식. 즉, 상위문제의 답을 구하기 위해 이전에 수행해야하는 절차를 수행하는 방식 (재귀함수로 구현)
- 동적계획법과 분할정복의 차이점은 나누어진 부분문제에 중복이 없다는 것과 하향식 접근법을 사용하고 메모이제이션 기법을 사용하지 않는다는 것
4. 탐욕 알고리즘(Greedy Algorithm)
- 최적의 해에 가까운 값을 구하기 위해 사용되는 알고리즘
- 여러가지 경우 중 하나를 결정해야할 때, 상황에 따라 매순간 최선의/최적의 선택을하여 최종적인 값을 구하는 방식
5. 백트래킹(Backtracking)
- 퇴각검색이라고 불리며, 제약조건 만족 문제(Constraint Satisfaction Problem)에서 해를 찾기 위한 전략
- 해를 찾기위해서 어떤 후보군을 대상으로 제약조건을 체크하다가 해당 후보군이 제약조건을 만족할 수 없다고 판단되면, 그 즉시 backtrack(다시는 해당 후보군을 체크하지 않을 것을 표시)한 후, 다른 후보군으로 넘어가는 방식으로 최적의 해를 찾는 전략
- 백트래킹에 의해 연산의 대상이 되는 후보군이 적어지고, 그만큼 시간복잡도가 줄어들어 빠르게 최적의 해를 찾을 수 있다.
해당 내용은 Do it! 자료구조와 함께 배우는 알고리즘 입문[자바편] 을 참고하여 정리했습니다.

'알고리즘' 카테고리의 다른 글
| [백준] 2609번 문제 풀이 - JAVA (0) | 2024.01.28 |
|---|---|
| [알고리즘] 알고리즘 - # 2. 배열과 자바 접근 (0) | 2023.02.23 |
| [알고리즘] 알고리즘 - #1.반복문 (0) | 2023.02.15 |


